Программирование : CD Interface ; Альтернативные решения | Конференция | Cсылки | Главная (фреймы)

Фракталы

см. также Turtle-графика
см. также Фракталы часть 2

Что же такое фрактал? Для начала давайте отвлечемся от математики и представим себе дерево. Мы видим ствол, на стволе- ветки, на ветках - ветки меньшего размера, и т.д. Сходная картина получается при рассмотрении фотографии горного ландшафта - при ближайшем рассмотрении становятся видны горы все меньшего и меньшего размера. Это ведь понятно. За все процессы, происходящие на Земле отвечает какая-то математика, которая вообщем-то одинакова для всех систем. Даже у человека все процессы контролирует математика. Вспомните как похожи кровеносные сосуды на ветвящееся растение. Так незаметно мы выявили, что все в природе САМОПОДОБНО. В некоторых пособиях самоподобие используется в качестве определяющего свойства фрактала.

Появление фракталов в математической литературе произошло около ста лет назад и было встречено с большой неприязнью. Во многом благодаря усилиям математика Бенуа Мандельброта фрактальная геометрия стала довольно значительной и уважаемой ветвью в математике. Он открыл большое количество фракталов, как то: фрактальное броуновское движение, флуктуации уровня рек и биения сердца. В большинстве трехмерных редакторах (3D Studio MAX, Animatec World Builder и др.) ландшафты генерируются с помощью фракталов.

В настоящее время фракталы проникают во все отрасли нашей жизни. Стали появляться, например, алгоритмы фрактального сжатия изображений.

Большая часть из предствленных здесь фракталов - Julia Set. Некоторая часть - Mandelbrot Set. Также есть алгоритм каждого фрактала.

Для начала давайте изучим исходный текст построения стандартного вида фрактала Julia Set.

Pascal

Uses graph;
var d,rt:integer;
i:longint;
wx,wy,cx,cy,x,y,m,n,r,theta:real;
begin
d:=Detect;
InitGraph(d,rt,'');
x:=GetMaxX;{ширина экрана}
y:=GetMaxY;{высота экрана}
for i:=1 to 100000 do {количество итераций}
begin
cx:=-1;cy:=0; {Константы вида}
wx:=x-cx;
wy:=y-cy;
if wx>0 then theta:=arctan(wy/wx);
if wx<0 then theta:=3.14159+arctan(wy/wx);
if wx=0 then theta:=1.57079; {pi/2}
theta:=theta/2;
r:=sqrt(wx*wx+wy*wy);
if Random<0.5 then
r:=sqrt(r)
else r:=-sqrt(r);
x:=r*cos(theta);
y:=r*sin(theta);
m:=-5+(x)*100+GetMaxX/2;
n:=(y)*100+GetMaxY/2;
PutPixel(trunc(m),trunc(n),White);
end;
outtext('Ok'); (Построение закончилось}
readln;
CloseGraph;
end.

Private Declare Function SetPixelV Lib "gdi32" (ByVal hdc As Long, ByVal x As Long, ByVal y As Long, ByVal crColor As Long) As Long
Public Sub JuliaSet()
x = picOut.Width: y = picOut.Height 'Размеры окна
For i = 1 To 100000
cx = -1: cy = 0
wx = x - cx
wy = y - cy
If wx > 0 Then theta = Atn(wy / wx)
If wx < 0 Then theta = 3.14159 + Atn(wy / wx)
If wx = 0 Then theta = 1.57079
theta = theta / 2
r = Sqr((wx) ^ 2 + (wy) ^ 2)
If Rnd < 0.5 Then r = Sqr(r) Else r = -Sqr(r)
x = r * Cos(theta)
y = r * Sin(theta)
m = (-5 + (x + 4) * 900 / 8)
n = ((2 - y) * 550 / 4)
SetPixelV picOut.hdc, m, n, 0
Next i
End Sub

У Вас должна получиться следующая картинка:

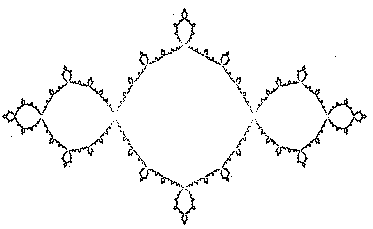
JuliaSet cx=-1;cy=0

Ну, теперь, когда Вы уже имеете понятие о JuliaSet можно чуть-чуть поэкспериментировать. Начнем с видового преобразования. В принципе достаточно изменять значения констант cx и cy, чтобы получить совершенно другой вид фрактала. Можно создавать целые библиотеки видов. Приведем несколько примеров:

cx	cy	Изображение
0.2	0.3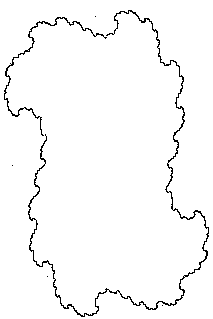
0	1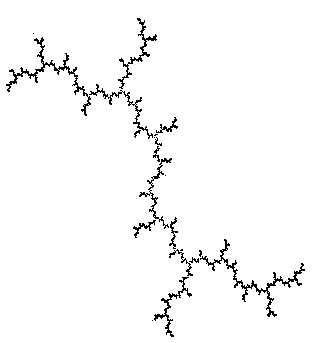
Cos(x)	x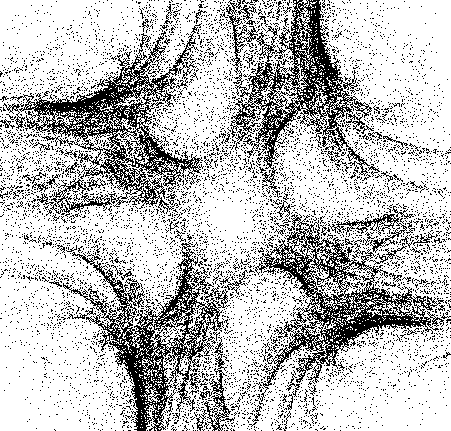

Теперь Вы сами можете создавать свои фракталы, интересные фигуры присылайте к нам на e-mail (в поле Subject укажите fractal), мы их обязательно опубликуем (естественно, с указанием авторства). Присылайте новые типы фракталов.

Еще один способ изменять вид фрактала - изменить алгоритм построения. Допустим, строку r=Sqr(wx^2+wy^2) можно изменить следующим образом: r = Sqr((wx + wy) ^ 2 + (wy + wx) ^ 2) , при этом получится следующий вид:

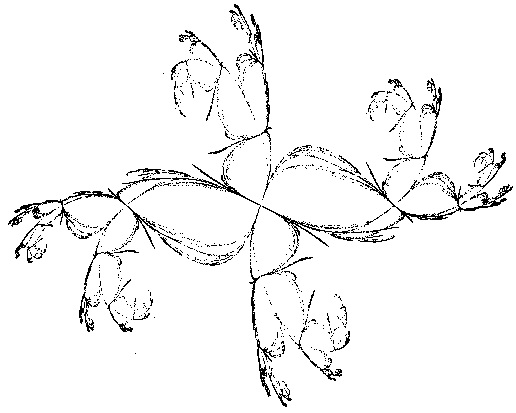
Далее мы приведем Вам некоторые изображения фракталов, а рядом-описание алгоритма их построения.

Изображения приведены в масштабе 1:2 (50%)

Описание	изображение
Количество итераций = 500'000 (рекомендую) Cx=-1;Cy=0 Модуль r=Sqr((wx + x) ^ 2 + (wy - y) ^ 2) Остальноe точно также как и начальном алгоритме
Количество итераций =128'000 (рекомендую) Cx=-0.3;Cy=0.2 Модуль r=Sqr((wx + x) ^ 2 + (wy - y) ^ 2) Остальное - то же.
Количество итераций =200'000 (рекомендую) Cx=0;Cy=0 Модуль r=Sqr((wx + x) ^ 2 + (wy - y) ^ 2) Остальное - то же.

Можно изменять также значения угла theta и многое многое другое...

Галерея фракталов

Еще одним типом фракталов является множество Мандельброта (Mandelbrot Set).

Для "совсем новичков" в этом деле можно посоветовать небольшое руководство, которое было переведено с английского Мещаниновым Николаем. Тут файл Ms Word97 (44 kb). Еще можно посоветовать очень неплохую программу ArosMagic Fractals ( http://www.ArosMagic.com ), которая строит три разных фрактала: Mandelbrot Set, Cubic Newton's Set, Plasma Cloud. Другие полезности см. раздел Link.

-получен программой ArosMagic Fractals

На VB строить фракталы довольно неприятно, но все же попробовать можно. Ниже - простейший алгоритм построения множества Мандельброта.

Private Declare Function SetPixelV Lib "gdi32" (ByVal hdc As Long, ByVal X As Long, ByVal Y As Long, ByVal crColor As Long) As Long
Dim MinX#, MaxX#, MinY#, MaxY#
Dim Coeff As Long
Dim CanIt As Boolean
Dim Last_a, Last_b, Last_c As Long
Dim MAX_ITERATION As Long
Dim canzoom As Boolean
Dim zX, zY As Long
Private Sub MandebrotlSet()
Static dx#, dy#
Static X%, Y%
Static color As Long
MinX# = CDbl(txtMin.Text) 'границы области вводит пользователь
MaxX# = CDbl(txtMax.Text)
MinY# = CDbl(txtMin1.Text)
MaxY# = CDbl(txtMax1.Text)
Coeff& = CLng(txtColor.Text)
MAX_ITERATION& = CLng(txtIt.Text)
dx# = (MaxX - MinY) / Mandel.ScaleWidth
dy# = (MaxY - MinY) / Mandel.ScaleHeight
CanIt = False
DoEvents
For Y% = 1 To Mandel.ScaleHeight - 1
   For X% = 1 To Mandel.ScaleWidth - 1
      color& = CalcPixel(MinX# + X% * dx#, MinY# + Y% * dy#)
      SetPixelV Mandel.hdc, X%, Y%, 16777215 - (color& / MAX_ITERATION&) * 16777215
      If CanIt = True Then Exit Sub
   Next
Mandel.Refresh
Next
Mandel.Refresh
End Sub
Function CalcPixel(ByVal cA As Double, ByVal cBi As Double) As Long
Static OLD_A#, A#, Bi#, Len_Z#
Static Iter As Long
A# = 0
Bi# = 0
Iter& = 0
Len_Z# = 0
DoEvents
Do Until (Len_Z# >= 4) Or (Iter& >= MAX_ITERATION&) Or CanIt = True
   OLD_A# = A#
   A# = A# * A# - Bi# * Bi# + cA#
   Bi# = 2 * OLD_A# * Bi# + cBi#
   Len_Z# = A# * A# + Bi# * Bi#
   Iter& = Iter& + 1
Loop
CalcPixel& = Iter&
End Function

Можно также скачать уже готовую программу здесь (с исходными текстами)

Программирование : CD Interface ; Альтернативные решения | Конференция | Cсылки | Главная (фреймы)

(обмен визитами)