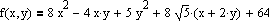Метод Нелдера-Мида
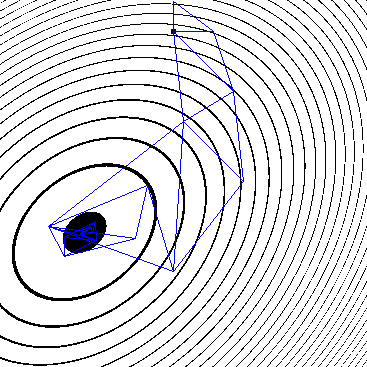
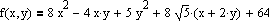
procedure TFrmMain.NelderMid(eps:double;fp:TWorldPoint);
const n=2;//размерность пространства
l=1;//длина ребра симплекса
alpha=1;//коэффициент отражения
beta=2;//коэффициент растяжения
gamma=0.5;//коэффициент сжатия
delta=0.5;//коэффициент редукции
type
TSimplexPoint=array [1..n] of double;
TSimplex=array[1..n+1] of TSimplexPoint;
var i,j,k:integer;
Simplex,NeoSimplex:TSimplex;
sp:TSimplexPoint;
p:TWorldPoint;
procedure ReenumerateVertexes(var NewSimplex:TSimplex);
//Делает правильную нумерацию вершин
var i,j:integer;
min:TSimplexPoint;
begin
for i:=1 to n+1 do
for j:=i+1 to n+1 do
if func(NewSimplex[j][1],NewSimplex[j][2])<func(NewSimplex[i][1],NewSimplex[i][2]) then
begin
min:=NewSimplex[i];
NewSimplex[i]:=NewSimplex[j];
NewSimplex[j]:=min;
end;
end;{ReenumerateVertexes}
procedure DrawSimplex(NewSimplex:TSimplex);
//Рисует Симплекс
var i:integer;
screen:TScreenPoint;
pnt:TWorldPoint;
begin
CopyScr.Canvas.pen.Color:=rgb(0,0,255);
Copyscr.Canvas.Pen.Mode:=pmCopy;
pnt.x:=NewSimplex[1][1];
pnt.y:=NewSimplex[1][2];
World2Screen(area,copyscr.Canvas.ClipRect,pnt,screen);
copyscr.Canvas.MoveTo(screen.x,screen.y);
for i:=2 to n+1 do
begin
pnt.x:=NewSimplex[i][1];
pnt.y:=NewSimplex[i][2];
World2Screen(area,copyscr.Canvas.ClipRect,pnt,screen);
copyscr.Canvas.LineTo(screen.x,screen.y);
end;
pnt.x:=NewSimplex[1][1];
pnt.y:=NewSimplex[1][2];
World2Screen(area,copyscr.Canvas.ClipRect,pnt,screen);
copyscr.Canvas.LineTo(screen.x,screen.y);
end;
procedure GetCenterPoint(gcpSimplex:TSimplex;var CenterPoint:TSimplexPoint);
//возвращает центральную точку грани(ребра) симплекса
var i,j:integer;
begin
for i:=1 to n do
begin
CenterPoint[i]:=0;
for j:=1 to n do
CenterPoint[i]:=CenterPoint[i]+gcpSimplex[j][i];//центр
CenterPoint[i]:=CenterPoint[i]/n;
end;{for i}
end;{GetCenterPoint}
function StopCond(NewSimplex:TSimplex):double;
{вычисляет функцию в условии останова}
var i:integer;
CenterPoint:TSimplexPoint;
begin
GetCenterPoint(NewSimplex,CenterPoint);
Result:=0;
for i:=1 to n+1 do
Result:=Result+sqr(func(Simplex[i][1],Simplex[i][2])-func(CenterPoint[1],CenterPoint[2]));
Result:=sqrt(Result/(n+1));
end;
begin
k:=1;
//строим начальный симплекс
{строим по центральной точке}
sp[1]:=fp.x;sp[2]:=fp.y;
{for i:=1 to n+1 do
for j:=1 to n do
begin
if j<i-1 then Simplex[i][j]:=sp[j];
if j=i-1 then Simplex[i][j]:=sp[j]+l*sqrt(j/(2*(j+1)));
if j>i-1 then Simplex[i][j]:=sp[j]-l/sqrt(2*j*(j+1));
end;}
{построение симплекса по базисным векторам}
Simplex[1]:=sp;
Simplex[2][1]:=sp[1]+l;
simplex[2][2]:=sp[2];
simplex[3][1]:=sp[1];
simplex[3][2]:=sp[2]+l;
ReenumerateVertexes(Simplex);
DrawSimplex(Simplex);
While StopCond(Simplex)>eps do
begin
//отражение
GetCenterPoint(Simplex,sp);
if (k mod RefreshRate)=0 then
begin
//fp.x нам уже не нужна - затираем, чтобы не вводить новых переменных
fp.x:=sin(60)*sqrt(sqr(Simplex[1][1]-Simplex[2][1])+sqr(Simplex[1][2]-Simplex[2][2]));
p.x:=Simplex[1][2]-Simplex[2][2];
p.y:=-Simplex[1][1]+Simplex[2][1];//перпендик к вектору Simplex[1]-Simplex[2]
Simplex[3][1]:=sp[1]+fp.x*p.x;
Simplex[3][2]:=sp[2]+fp.x*p.y;
// fp.x:=sp[1];fp.y:=sp[2];
// SetPoint(fp);
// DrawSimplex(Simplex);
end;
// fp.x:=sp[1];fp.y:=sp[2];
NeoSimplex:=Simplex;
for i:=1 to n do
NeoSimplex[n+1][i]:=sp[i]+alpha*(sp[i]-Simplex[n+1][i]);
if func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])<func(Simplex[1][1],Simplex[1][2]) then
begin
//этап 2 - растяжение
Simplex:=NeoSimplex;
GetCenterPoint(Simplex,sp);
NeoSimplex:=Simplex;
for i:=1 to n do
NeoSimplex[n+1][i]:=sp[i]+beta*(Simplex[n+1][i]-sp[i]);
if func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])<func(Simplex[1][1],Simplex[1][2]) then
Simplex:=NeoSimplex;
DrawSimplex(Simplex);
ReenumerateVertexes(Simplex);
inc(k);
continue;
end;
if (func(NeoSimplex[n][1],NeoSimplex[n][2])>=func(NeoSimplex[n+1][1],NeoSimplex[n+1][2]))
and (func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])>=func(NeoSimplex[1][1],NeoSimplex[1][2])) then
begin
DrawSimplex(NeoSimplex);
Simplex:=NeoSimplex;
ReenumerateVertexes(Simplex);
inc(k);
continue;
end;
if (func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])>func(NeoSimplex[n][1],NeoSimplex[n][2]))
and (func(NeoSimplex[n][1],NeoSimplex[n][2])>=func(NeoSimplex[1][1],NeoSimplex[1][2])) then
//сжатие нового симплекса
begin
GetCenterPoint(NeoSimplex,sp);
if func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])<=func(Simplex[n+1][1],Simplex[n+1][2]) then
//Проверить возможность прсчета центральной точки в неосимплексе -
//должно ли быть безразлично где считать? Да
for i:=1 to n do
NeoSimplex[n+1][i]:=sp[i]+gamma*(NeoSimplex[n+1][i]-sp[i])
else
for i:=1 to n do
NeoSimplex[n+1][i]:=sp[i]+gamma*(Simplex[n+1][i]-sp[i]);
if func(NeoSimplex[n+1][1],NeoSimplex[n+1][2])<func(Simplex[n+1][1],Simplex[n+1][2]) then
begin
Simplex:=NeoSimplex;
ReenumerateVertexes(Simplex);
DrawSimplex(Simplex);
inc(k);
continue;
end
else
begin
//редукция симплекса
for i:=2 to n+1 do
for j:=1 to n do
NeoSimplex[i][j]:=Simplex[1][j]+delta*(Simplex[i][j]-Simplex[1][j]);
Simplex:=NeoSimplex;
ReenumerateVertexes(Simplex);
DrawSimplex(Simplex);
inc(k);
continue;
end;
end;
end;{while}
ReenumerateVertexes(Simplex);
fp.x:=Simplex[1][1];
fp.y:=Simplex[1][2];
BuiltReport(fp,fp,k,0);
end;