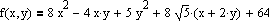Метод Хука-Дживса
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
|
| 1 | (-3.727,-1.491) | 44.000 |
| 2 | (-1.622,-3.595) | -31.294 |
| 3 | (-1.622,-4.227) | -33.287 |
| 4 | (-2.175,-4.227) | -35.729 |
| 5 | (-2.175,-4.448) | -35.973 |
| 6 | (-2.230,-4.448) | -35.997 |
| 7 | (-2.230,-4.470) | -36.000
 |
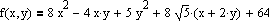
procedure TfrmMain.HookJeavse(eps:double;fp:TWorldPoint);
const n=2;
var wavex,xkwave,lastxkwave,curx,b:TWorldPoint;
basis:array [1..n] of TWorldPoint;
screen:TScreenPoint;
fmj,fpj,fjk,gamma,a:double;//f_{-j},f_{+j},...
k,j:integer;
begin
basis[1].x:=1;basis[1].y:=0;
basis[2].x:=0;basis[2].y:=1;
b.x:=1;b.y:=1;
gamma:=2;
curx:=fp;{нормальные к-ые точки (используются после исчерпывающего спуска)}
wavex:=fp;{x с волной и с нижним индексом-промежуточные точки}
xkwave:=fp;{x с волной без нижнего индекса}
k:=1;
while true do
begin
while (xkwave.x=wavex.x) and (xkwave.y=wavex.y) do
begin
for j:=1 to n do {двигаемся по базисным векторам}
begin
fjk:=func(wavex.x,wavex.y);
fpj:=func(wavex.x+b.x*basis[j].x,wavex.y+b.y*basis[j].y);
fmj:=func(wavex.x-b.x*basis[j].x,wavex.y-b.y*basis[j].y);
if (fjk>fpj) and (fmj>=fpj) then
begin
wavex.x:=wavex.x+b.x*basis[j].x;
wavex.y:=wavex.y+b.y*basis[j].y;
end
else if (fjk>fmj) and (fpj>fmj) then
begin
wavex.x:=wavex.x-b.x*basis[j].x;
wavex.y:=wavex.y-b.y*basis[j].y;
end;
World2Screen(Area,CopyScr.Canvas.ClipRect,wavex,Screen);
CopyScr.Canvas.LineTo(Screen.x,Screen.y);
SetPoint(wavex);
pbOut.Refresh;
end;{for j}
if (xkwave.x=wavex.x) and (xkwave.y=wavex.y) then
begin
b.x:=b.x/gamma;
b.y:=b.y/gamma;
end;
if sqrt(sqr(b.x)+sqr(b.y))<eps then
begin
BuiltReport(xkwave,wavex,k,0);//минимум найден
exit;
end;
end;{while xkwave=wavex}
if abs(func(xkwave.x,xkwave.y)-func(wavex.x,wavex.y))<eps then break;
lastxkwave:=xkwave;
xkwave:=wavex;
xk:=curx; {для исчерпывающего спуска}
uk.x:=xkwave.x-lastxkwave.x; uk.y:=xkwave.y-lastxkwave.y;
a:=MakeDichotomy(0,100,1e-5,eps/100,Pseudo1D);{реализуем исчерпывающий спуск}
curx.x:=lastxkwave.x+a*(xkwave.x-lastxkwave.x); //todo : replace to uk
curx.y:=lastxkwave.y+a*(xkwave.y-lastxkwave.y);
World2Screen(Area,CopyScr.Canvas.ClipRect,curx,Screen);
CopyScr.Canvas.LineTo(Screen.x,Screen.y);
SetPoint(curx);
pbOut.Refresh;
BuiltReport(curx,xkwave,k,0);
wavex:=curx;
xkwave:=curx;
inc(k);
end;{while}
end;