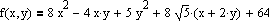Метод наискорейшего спуска
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
| | антиградиент |
| 1 | (-1.001,-4.270) | -24.590 | 0.112 | (-8.944,-58.138) |
| 2 | (-2.112,-4.099) | -35.365 | 0.059 | (-18.953,2.916) |
| 3 | (-2.167,-4.461) | -35.965 | 0.112 | (-0.498,-3.236) |
| 4 | (-2.229,-4.451) | -35.998 | 0.059 | (-1.055,0.162) |
| 5 | (-2.232,-4.472) | -36.000 | 0.112 | (-0.028,-0.180) |
| 6 | (-2.236,-4.471) | -36.000 | 0.059 | (-0.059,0.009) |
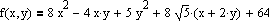
procedure TfrmMain.QuickestDescent(eps:double;fp:TWorldPoint);
var grad:TWorldPoint;
curx,lastx:TWorldPoint;
funcs:T1DFunction;
screen1:TScreenPoint;
cappa:double;
k:integer;
begin
curx:=fp;
lastx:=fp;
lastx.x:=lastx.x+23;//для отличия от fp
GradientFunc(fp.x,fp.y,grad);
funcs:=@Pseudo1D;
k:=1;
while abs(Func(curx.x,curx.y)-Func(lastx.x,lastx.Y))>eps do
begin
GradientFunc(curx.x,curx.y,grad);
xk:=curx;
uk:=grad;
//Исчерпывающий спуск в выбранном направлении
cappa:=MakeDichotomy(0,1,1e-5,eps/100,funcs);{Более подробно о дихотомии можно прочитать
здесь, а исходный текст этой процедуры можно посмотреть здесь}
lastx:=curx;
curx.x:=curx.x+cappa*grad.x;
curx.y:=curx.y+cappa*grad.y;
BuiltReport(curx,grad,k,cappa);//Добавление строк в таблицу итераций
//Построение звена тракетории поиска
World2Screen(Area, copyscr.Canvas.ClipRect,curx,screen1);
SetPoint(curx);
copyscr.Canvas.LineTo(screen1.x,screen1.y);
inc(k);
end;
end;