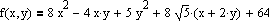Метод Давидона-Флетчера-Пауэлла (ДФП-метод)
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
| | антиградиент |
| 1 | (-1.001,-4.270) | -24.590 | 0.112 | (-18.953,2.916) |
2 | (-2.236,-4.472) | -36.000 | 0.069 | (0.000,0.000)
 |
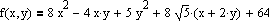
procedure TfrmMain.DFPMethod(eps:double;fp:TWorldPoint);
type
TDoubleMatrix=array[0..1] of array [0..1] of double;
var k:integer;
grad,lastgrad,curx,lastx,pk,
Deltax,DeltaW:TWorldPoint;
cappa,alpha,beta:double;
screen1:TScreenPoint;
Ak,A:TDoubleMatrix;
const E:TDoubleMatrix=((1,0),(0,1));
begin
Ak:=E;
GradientFunc(fp.x,fp.y,grad);
curx:=fp;
lastgrad:=grad;
k:=1;
while sqrt(sqr(grad.x)+sqr(grad.y))>eps do
begin
pk.x:=Ak[0][0]*grad.x+Ak[0][1]*grad.y; //Ak*(-grad(curx))
pk.y:=Ak[1][0]*grad.x+Ak[1][1]*grad.y;
xk:=curx;
uk:=pk;
//Подробнее об использовании дихотомии и процедуры MakeDichotomy читайте здесь
cappa:=MakeDichotomy(0,100,1e-5,eps/100,Pseudo1D);
LastX:=curx;
curx.x:=curx.x+cappa*pk.x;
curx.y:=curx.y+cappa*pk.y;
Lastgrad:=grad;
GradientFunc(curx.x,curx.y,grad);
BuiltReport(curx,grad,k,cappa);
SetPoint(curx);
World2Screen(Area, copyscr.Canvas.ClipRect,curx,screen1);
copyscr.Canvas.LineTo(screen1.x,screen1.y);
if (k mod RefreshRate)=0 then
Ak:=E
else
begin
DeltaX.x:=curx.x-lastx.x;
DeltaX.y:=curx.y-lastx.y;
DeltaW.x:=grad.x-lastgrad.x;
DeltaW.y:=grad.y-lastgrad.y;
//Построение матрицы А. Возможно, не совсем хорошо осуществленно...
A:=Ak;
alpha:=1/(deltaw.x*deltax.x+deltaw.y*deltax.y);
beta:=1/((A[0][0]*deltaw.x+A[0][1]*deltaw.y)*deltaw.x+(A[1][0]*deltaw.x+A[1][1]*deltaw.y)*deltaw.y);
Ak[0][0]:=A[0][0]-alpha*sqr(deltax.x)-beta*(
sqr(A[0][0]*deltaw.x)+
2*A[0][0]*deltaw.x*A[0][1]*deltaw.y+
sqr(A[0][1]*deltaw.y));
Ak[0][1]:=A[0][1]-alpha*deltax.x*deltax.y-beta*(
A[0][0]*sqr(deltaw.x)*A[1][0]+
A[0][0]*deltaw.x*A[1][1]*deltaw.y+
A[0][1]*deltaw.y*A[1][0]*deltaw.x+
A[0][1]*sqr(Deltaw.y)*A[1][1]);
Ak[1][0]:=A[1][0]-alpha*deltax.x*deltax.y-beta*(
A[0][0]*sqr(deltaw.x)*A[1][0]+
A[0][0]*deltaw.x*A[1][1]*deltaw.y+
A[0][1]*deltaw.y*A[1][0]*deltaw.x+
A[0][1]*sqr(Deltaw.y)*A[1][1]);
Ak[1][1]:=A[1][1]-alpha*sqr(deltax.y)-beta*(
sqr(A[1][0]*deltaw.x)+
2*A[1][0]*deltaw.x*A[1][1]*deltaw.y+
sqr(A[1][1]*deltaw.y));
end;
inc(k);
end;
end;