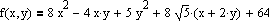Метод циклического покоординатного спуска
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
| |
| 1 | (-0.559,-3.801) | -15.750 | -6.037 |
| 2 | (-2.068,-4.405) | -35.797 | -0.604 |
| 3 | (-2.219,-4.465) | -35.998 | -0.060 |
| 4 | (-2.234,-4.471) | -36.000 | -0.006 |
| 5 | (-2.236,-4.472) | -36.000 | -0.001 |
| 6 | (-2.236,-4.472) | -36.000 | -0.000 |
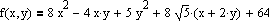
procedure TFrmMain.CycledDescent(eps:double;fp:TWorldPoint);
const n=2;
type TNDimensionalVector=array[1..n] of double;
var j,k:integer;
basis:array[1..n] of TNDimensionalVector;
curx,lastcoordx,tmpx,lastx:TNDimensionalVector;
screen:TScreenPoint;
alpha:double;
begin
basis[1][1]:=1;basis[1][2]:=0;
basis[2][1]:=0;basis[2][2]:=1;
curx[1]:=fp.x;curx[2]:=fp.y;
k:=1;
while true do
begin
lastcoordx:=curx;
tmpx:=curx;
for j:=1 to n do
begin
xk.x:=lastcoordx[1];xk.y:=lastcoordx[2];
uk.x:=basis[j][1];uk.y:=basis[j][2];
alpha:=MakeDichotomy(-10,10,1e-5,eps/100,Pseudo1D);
tmpx[1]:=tmpx[1]+alpha*basis[j][1];
tmpx[2]:=tmpx[2]+alpha*basis[j][2];
fp.x:=tmpx[1];fp.y:=tmpx[2];
World2Screen(area,copyscr.Canvas.ClipRect,fp,screen);
copyscr.Canvas.LineTo(screen.x,screen.y);
setpoint(fp);
lastcoordx:=tmpx;
end;
lastx:=curx;
curx[1]:=tmpx[1]+alpha*basis[n][1];
curx[2]:=tmpx[2]+alpha*basis[n][1];
BuiltReport(fp,fp,k,alpha);
fp.x:=curx[1];fp.y:=curx[2];
World2Screen(area,copyscr.Canvas.ClipRect,fp,screen);
copyscr.Canvas.LineTo(screen.x,screen.y);
setpoint(fp);
if sqrt(sqr(curx[1]-lastx[1])+sqr(curx[2]-lastx[2]))<eps then break;
inc(k);
end;
end;