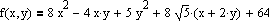Градиентный спуск с дроблением шага
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
| | антиградиент |
| 1 | (-0.559,-1.398) | 13.141 | 0.063 | (-8.944,-58.138) |
| 2 | (-1.467,-2.900) | -23.748 | 0.063 | (-14.534,-24.038) |
| 3 | (-1.843,-3.690) | -32.937 | 0.063 | (-6.009,-12.648) |
| 4 | (-2.041,-4.081) | -35.234 | 0.063 | (-3.162,-6.245) |
| 5 | (-2.138,-4.276) | -35.809 | 0.063 | (-1.561,-3.132) |
| 6 | (-2.187,-4.374) | -35.952 | 0.063 | (-0.783,-1.565) |
| 7 | (-2.212,-4.423) | -35.988 | 0.063 | (-0.391,-0.783) |
| 8 | (-2.224,-4.448) | -35.997 | 0.063 | (-0.196,-0.391) |
| 9 | (-2.230,-4.460) | -35.999 | 0.063 | (-0.098,-0.196) |
| 10 | (-2.233,-4.466) | -36.000 | 0.063 | (-0.049,-0.098) |
| 11 | (-2.235,-4.469) | -36.000 | 0.063 | (-0.024,-0.049) |
| 12 | (-2.235,-4.471) | -36.000 | 0.063 | (-0.012,-0.024) |
| 13 | (-2.236,-4.472) | -36.000 | 0.125 | (-0.006,-0.012) |
| 14 | (-2.236,-4.472) | -36.000 | 0.000 | (-0.000,0.000)  |
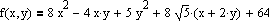
procedure TfrmMain.FastFallWithCrackingStep(eps:double;fp:TWorldPoint);
var k:integer;
gamma,cappa:double;
lastx,x,grad:TWorldPoint;
Screen2:TScreenPoint;
const cappa0=1;
begin
k:=1;gamma:=0.5;//gamma - Коэффициент дробления шага
x:=fp;//fp - начальная точка
lastx:=fp;
GradientFunc(fp.x,fp.y,grad);//вычисляем антиградиент функции
//Условие останова - длина вектора (анти)градиента меньше заданной точности eps
while sqrt(sqr(grad.x)+sqr(grad.y))>eps do
begin
cappa:=cappa0;
GradientFunc(lastx.x,lastx.y,grad);
x.x:=lastx.x+cappa*grad.x;
x.y:=lastx.y+cappa*grad.y;
while Func(lastx.x,lastx.y)-Func(x.x,x.y)<0.5*cappa*(sqr(grad.x)+sqr(grad.y)) do
begin
cappa:=cappa*gamma;
x.x:=lastx.x+cappa*grad.x;
x.y:=lastx.y+cappa*grad.y;
end;
BuiltReport(x,grad,k,cappa);//Вывод отчета об итерациях
//Построение звена траектории спуска
World2Screen(Area, copyscr.Canvas.ClipRect,x,screen2);
SetPoint(x);
lastx:=x;
copyscr.Canvas.LineTo(screen2.x,screen2.y);
inc(k);//Счетчик итераций
end;{while}
end;