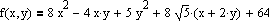Метод сопряженных направлений
Таблица итераций
(точность eps=10e-3)
| Номер итерации | |
| | антиградиент |
| 1 | (-1.001,-4.270) | -24.590 | 0.112 | (-18.953,2.916) |
| 2 | (-2.236,-4.472) | -36.000 | 0.062 | (0.000,-0.000)
 |
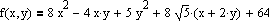
procedure TfrmMain.ConjDirection(eps:double;fp:TWorldPoint);
var k:integer;
grad,lastgrad,curx,lastx,pk:TWorldPoint;
cappa,gamma:double;
screen1:TScreenPoint;
//Сопряженных направлений
begin
curx:=fp;
GradientFunc(fp.x,fp.y,grad);
pk:=grad;
k:=1;
while sqrt(sqr(grad.x)+sqr(grad.y))>eps do
begin
xk:=curx;
uk:=pk;
//Подробнее об использовании дихотомии и процедуры MakeDichotomy читайте здесь
cappa:=MakeDichotomy(0,10,1e-5,eps/100,Pseudo1D);
lastx:=curx;
curx.x:=curx.x+cappa*pk.x;
curx.y:=curx.y+cappa*pk.y;
Lastgrad:=grad;
GradientFunc(curx.x,curx.y,grad);
BuiltReport(curx,grad,k,cappa);
SetPoint(curx);
World2Screen(Area, copyscr.Canvas.ClipRect,curx,screen1);
copyscr.Canvas.LineTo(screen1.x,screen1.y);
//Проверка на принадлежность номера итерации к множеству точек рестарта
//RefreshRate - описана как глобальная переменная
if (k mod RefreshRate)=0 then
pk:=grad
else
begin
gamma:=(sqr(grad.x)+sqr(grad.y))/(sqr(lastgrad.x)+sqr(lastgrad.y));
pk.x:=gamma*pk.x+grad.x;
pk.y:=gamma*pk.y+grad.y;
end;
inc(k);
end;{while}
end;