Об ошибках вычисления
Рассмотрим следующий пример.
Допустим, нам необходимо вычислить интеграл
(1)
При этом, условимся, что мы,якобы, не знаем как вычислять интегралы численно. Поэтому, после нетрудных выкладок

получаем рекуррентное соотношение:
,

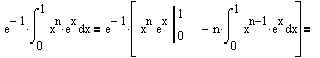
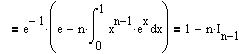
Которое и будем использовать для написания программы вычисления исходного интеграла. Приведем код на Delphi, но, при желании, можно будет использовать любой другой язык.
paradox.pas - вычисление интеграла, используя прямое рекуррентное соотношение 
const e=2.7182818284590452353602874713527;
In0=1-1/e;
var j:integer;
    Intn:double;
begin
Intn:=In0;
for j:=1 to 20 do {20 - это число n -его можно изменить}
begin
        Intn:=1-j*Intn;{реализация рекуррентной формулы}
        writeln(Intn);
end;
end.
Результат выполнения этой программы отображен слева. Справа- истинные значения:
Номер Результат выполнения прямого рекуррентного алгоритма Истинные(если так можно сказать) значения, вычисленные численно
 1.
 2.
 3.
 4.
 5.
 6.
 7.
 8.
 9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
 3.67879441171442E-0001
2.64241117657115E-0001
2.07276647028654E-0001
1.70893411885384E-0001
1.45532940573080E-0001
1.26802356561520E-0001
1.12383504069363E-0001
1.00931967445092E-0001
9.16122929941707E-0002
8.38770700582927E-0002
7.73522293587803E-0002
7.17732476946367E-0002
6.69477799697233E-0002
6.27310804238732E-0002
5.90337936419019E-0002
5.54593017295701E-0002
5.71918705973076E-0002
-2.94536707515363E-0002
1.55961974427919E+0000
-3.01923948855838E+0001
 3.67879441171442E-01
2.64241117657115E-01
2.07276647028654E-01
1.70893411885384E-01
1.45532940573079E-01
1.26802356561528E-01
1.12383504069301E-01
1.00931967445593E-01
9.16122929896606E-02
8.38770701033942E-02
7.73522288626642E-02
7.17732536480296E-02
6.69477025756157E-02
6.27321639413802E-02
5.90175408792978E-02
5.57193459312356E-02
5.27711191689948E-02
5.01198549580943E-02
4.77227557962091E-02
4.55448840758181E-02
Видно, что, начиная с некоторого номера (в последних разрядах - с четвертого), значения начинают сильно разниться. А в последних строчках разница вообще принципиальная! Но ведь алгоритм вроде бы разработан правильно!
Все дело в том, что первоначальное значение I0 было вычислено с некоторой, пусть малой, но ошибкой. В последствии, наш алгоритм, используя этот результат, накапливал ошибку, превращая, в конце концов, все вычисление в абсурдное занятие. Давайте оценим значение ошибки, возникающей в этом случае. Пусть
- абсолютная ошибка вычисления I0. Поскольку при вычитании абсолютные ошибки складываются, имеем:
.
Таким образом, первоначальная ошибка возрастает в n! раз!!! Понятно, что при больших n результат выполнения вышеизложенного алгоритма даст даже не приблизительные результаты.
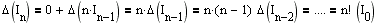Заметим, однако, следующий факт:
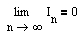
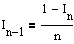
Это нам позволит обратить нашу рекуррентную формулу следующим образом:
Поэтому, для увеличения точности, будем двигаться "сверху вниз", положив для достаточно больших n In=0. Такой алгоритм можно реализовать, например так:
GetCallBackIntegral.pas - вычисление обратным рекуретным способом 
function GetCallBackIntegral(n:integer):double;
var i:integer;
      Intn:double;
begin
Intn:=0;
for i:=10*n downto n+1 do {конечно грубо...}
       Intn:=(1-Intn)/i;
result:=Intn;
end;
Сравним работу такого алгоритма с эталоном:
Номер Результат работы обратного рекуррентного алгоритма Эталон
 1.
 2.
 3.
 4.
 5.
 6.
 7.
 8.
 9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
 3.67879464285714E-0001
2.64241117657115E-0001
2.07276647028654E-0001
1.70893411885384E-0001
1.45532940573079E-0001
1.26802356561528E-0001
1.12383504069300E-0001
1.00931967445593E-0001
9.16122929896606E-0002
8.38770701033942E-0002
7.73522288626642E-0002
7.17732536480296E-0002
6.69477025756157E-0002
6.27321639413801E-0002
5.90175408792978E-0002
5.57193459312356E-0002
5.27711191689948E-0002
5.01198549580943E-0002
4.77227557962091E-0002
4.55448840758181E-0002
 3.67879441171442E-01
2.64241117657115E-01
2.07276647028654E-01
1.70893411885384E-01
1.45532940573079E-01
1.26802356561528E-01
1.12383504069301E-01
1.00931967445593E-01
9.16122929896606E-02
8.38770701033942E-02
7.73522288626642E-02
7.17732536480296E-02
6.69477025756157E-02
6.27321639413802E-02
5.90175408792978E-02
5.57193459312356E-02
5.27711191689948E-02
5.01198549580943E-02
4.77227557962091E-02
4.55448840758181E-02
Не знаю как Вам, а мне его работа несколько больше нравится :-).
Итак. Казалось бы разница в выражениях

и
с математической точки зрения небольшая, но одно из них дает "устойчивый" алгоритм (т.е. ошибка в нем накапливается незначительно), а второе - неустойчивый.
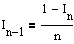
Мещанинов Николай по результатам семинара "Методы вычислений" Галанина М.П.(МГТУ им. Н.Э. Баумана, Фн12)
Hosted by uCoz